最近、スト鯖RustことVCR Rustを楽しく見てます。
で、いろんな人がルーレットで金を溶かしたり儲けたりしてるんだけど、必勝法あるんじゃね?というのが気になったので調べてみてた。
結論からいうと、必勝法はありそう。
(2023/5/7追記)必勝法(期待値がプラスになる賭け方)はありましたが、その後、5月のアップデートでルーレットの挙動が変わり、この方法で勝率を上げることはできなくなったようです。何かに応用できる可能性はあるので記事自体は消さずに残しますが、直接的に役立つことはないと思います。
筆者はこの記事を書いた後、実際にRustを購入してスクラップを増やせるのか実験しました。アップデート前に、100スクラップから1000スクラップに(つまり10倍に)増やすことに成功しましたが、アップデート後は回転数が明らかに変化したため、不可能と判断して実験を中断しました。
アップデートがなければ、確率論的に最も効率よくスクラップを増やす賭け率などの考察の記事を書くつもりでしたが、それも諦めました。期待値がプラスになる賭けがある場合に、どのような賭け方をするとリスクと効率のバランスが取れるのか、持ち金がいくらの場合にどの程度の破産リスクがあるのか、ということを調べたい場合、「ケリー基準」や「バルサラの破産確率表」といったキーワードで調べてみると役に立つと思います。
ただ、効率が良いかというと、まあどうなんだろうね。
なお、筆者はエアプ勢です。ネットでちょこっとググって分かる範囲でしかRustを知りません。
どんな必勝法?
上の動画の5:19くらいから解説してくれてます。(英語)
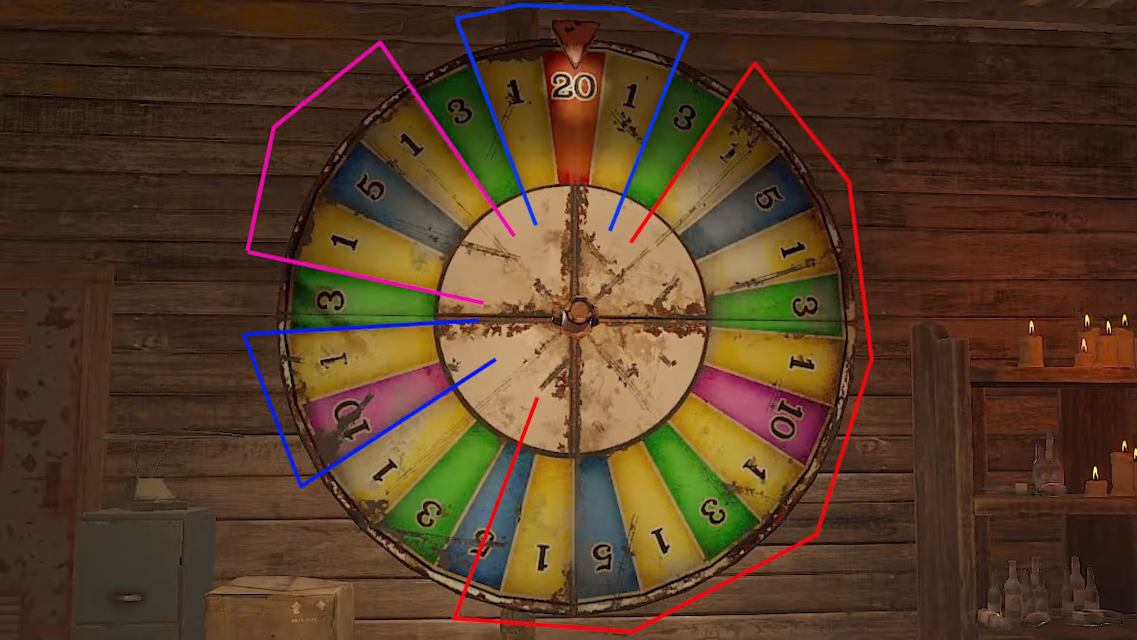
簡単に説明すると、上の画像の
- 青枠の箇所で止まっていたら5に賭ける
- ピンク枠の箇所で止まっていたら10に賭ける
- 赤枠の箇所に止まっていたら20に賭ける
というものです。
賭けたから必ず当たるわけではないんですが、少し確率が高くなっているとのこと。
なんで? なんでこれで勝てるの?
なぜか、というのも上の動画で解説してくれています。
まず、Rustのルーレットは「一定範囲のランダムな速度を与えて回転をはじめる」という実装になっています。
このことは上の動画内で実際のコードを示して説明されていますし、例えばRedditの以下の投稿でもそのように説明されています。
How a Rust server generates roulette spins : playrust
さて、回転を始めるときの初速度は一様に分布していますが、結果として何回転するか?というと、最小で「4回転+2目盛」から最大で「5回転半+2目盛」の間になります。
したがって、元の位置から2目盛〜半回転+2目盛分動く可能性は、残りの半分より確率がおおよそ倍程度大きくなっているのです。動画内でも、以下の図で解説されています。

このことから、回転前の状態から確率の高い数字を選びます。
つまり、5,10,20が「元の位置から2目盛〜半回転+2目盛」の領域に含まれる(または多く含まれる)ときに賭ける、という戦略になります。
1や3はルーレット盤全体にまんべんなく存在しているため、偏りのある5,10,20を対象とします。
厳密には、初速度が一様分布であったとしても、結果の回転角度が一様分布してるわけでは無いはずですが、ここでは簡単のため、一様分布として考えます。
(ちゃんと計算したわけじゃないけど、厳密には平方根の逆数に比例する分布になっているんじゃないかと思います。若干ですが、回転数が少ないほうに確率が偏っているはずです。)
この方法を使った場合の期待値はどんなもん?
各パターンの期待値は次のようになるはずです。
パターン |
倍率の期待値 |
|---|---|
青枠の箇所で止まっていたら5に賭ける |
1.12 |
ピンク枠の箇所で止まっていたら10に賭ける |
1.17 |
赤枠の箇所に止まっていたら20に賭ける |
1.12 |
期待値の計算
以下、それぞれの計算過程を記します。
前提として、確率が高めな半分の領域に止まる確率を2/3(66.7%)、確率低めな領域に止まる確率を1/3(33.3%)と仮定します。
領域半分はいずれも12.5マス分と仮定します。
青枠の箇所で止まっていたら5に賭ける
倍率の期待値は1.12です。
つまり、たとえばスクラップ100を賭け続けた場合、当たる場合も当たらない場合もありますが、平均して1回あたり12ずつ増えていく、ということになります。
以下に計算過程を示します。
まず、確率高めな半分の領域に止まる確率2/3、さらにこの半分の領域に5のマスは3つありますから、確率高めな半分かつ5にとまる確率は2/3*3/12.5。
同様に、確率低めな半分にある5のマス(1か所だけありますね)にとまる確率は1/3*1/12.5。
上の2つを足し合わせて、5が出る確率は18.7%となります。
倍率の期待値は(1+5)*(2/3*3/12.5+1/3*1/12.5)=1.12となります。
ピンク枠の箇所で止まっていたら10に賭ける
倍率の期待値は1.17です。
以下が計算過程です。
このパターンでは、確率高めな半分の領域に10が2マスある場合に賭ける、ということになります。
(もう半分の領域には10のマスはありません)
したがって、10のマスにとまる確率は2/3*2/12.5=10.7%となり、倍率の期待値は(1+10)*2/3*2/12.5=1.17となります。
赤枠の箇所に止まっていたら20に賭ける
倍率の期待値は1.12です。
以下が計算過程です。
このパターンでは、確率高めな半分の領域に20のマスある場合に賭ける、ということになります。
20のマスにとまる確率は2/3*1/12.5=5.3%となり、倍率の期待値は(1+20)*2/3*1/12.5=1.12となります。
てか、期待値渋すぎない?
単純に適当に賭けるより、かなり確率が上がるはずのズルしてようやくこの期待値ってなんやねん。。。とは思う。
また、上の動画のコメント欄でも、実際にやってみてうまく行った、うまく行かなかった、みたいな体験談が色々書かれてる。
実際に実行するとなると、単に期待値だけでなく、バラつき具合も重要になる。
種銭がそれなりにないときついだろうなあ。
この方法を使わず、どのマスに止まる確率も偏りなく分布してると仮定すると、期待値はこんな感じ。
番号 |
倍率 |
マス数 |
的中率 |
期待値 |
|---|---|---|---|---|
1 |
2 |
12 |
48.0% |
0.96 |
3 |
4 |
6 |
24.0% |
0.96 |
5 |
6 |
4 |
16.0% |
0.96 |
10 |
11 |
2 |
8.0% |
0.88 |
20 |
21 |
1 |
4.0% |
0.84 |
ま、ギャンブルで儲けようなんて、普通はそんなうまくいくわけないもんねえ・・・笑
